Conversor de Grados a Radianes o (π rad)

De:

rad

Fórmula y resultado en 𝜋 rad

= \frac{1^{\circ} \cdot π r a d}{180^{\circ}}

¿Cómo calcular grados a radianes?

Para realizar el cálculo, tengamos en cuenta que 𝜋 radianes es igual a 180 grados.

La conversión de grados a radianes es una operación matemática común en diversas disciplinas como la física, la ingeniería y las matemáticas.

Conceptos Básicos

Grado: Es una unidad de medida de ángulos. Un círculo completo tiene 360 grados.
- El símbolo de los grados es “°”

Radián: Es otra unidad de medida de ángulos. Un círculo completo tiene 2π radianes.
- El símbolo de los radianes es la abreviatura “rad” o “𝜋rad”

Nota En los cálculos con radianes, el número pi (𝜋) aparece frecuentemente. Debemos acostumbrarnos a trabajar con 𝜋 porque es un número irracional, lo que significa que no puede expresarse como una fracción exacta y su valor decimal se extiende infinitamente sin repetirse. Si aproximamos 𝜋 a un número decimal, perdemos precisión en los cálculos. Por esta razón, es común dejar los resultados en términos de 𝜋rad para mantener la exactitud.

Fórmulas de Conversión

Para convertir grados a radianes, se utilizará la siguiente fórmula:

radianes = grados x \frac{𝜋}{180}

Esta fórmula se deriva del hecho de que un círculo completo tiene 360 grados o 2π radianes. Al simplificar la proporción, se obtiene que 1 grado es equivalente a 𝜋/180 radianes.

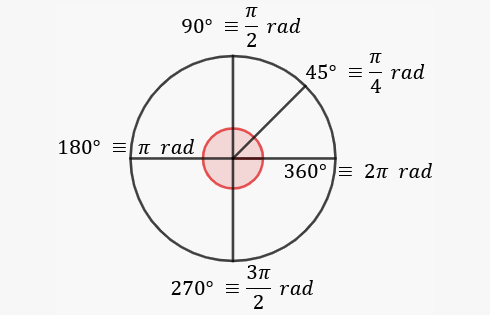
Conversión de grados a radianes — Relación grados – radianes

Teniendo en cuenta que la relación entre grados y radianes es de proporcionalidad directa, vamos a simplificar la fórmula de cálculo mediante una regla de tres directa.

Por ejemplo, si queremos convertir 20° a radianes, aplicamos una regla de tres sabiendo que 180° es igual a π radianes.

Grados	Radianes
180°	π rad
20°	𝑥

Ahora bien, para hallar 𝑥 sería de la siguiente manera:

x = \frac{20^{\circ} \cdot π r a d}{180^{\circ}}

Ahora que tenemos la fórmula inicial, solo nos faltaría simplificar los valores. Veamos algunos ejemplos.

Ejemplos de conversión

Convertir 90 grados a radianes.

\frac{90^{\circ} \cdot π r a d}{180^{\circ}} = \frac{1}{2} \cdot π r a d

Por lo tanto, 90° es igual 1/2 π radianes.

Si queremos hallar el valor en radianes y no en términos de 𝜋, debemos reemplazar el valor de π